백준 1956 - 운동(C++)

문제 링크입니다. https://www.acmicpc.net/problem/1956

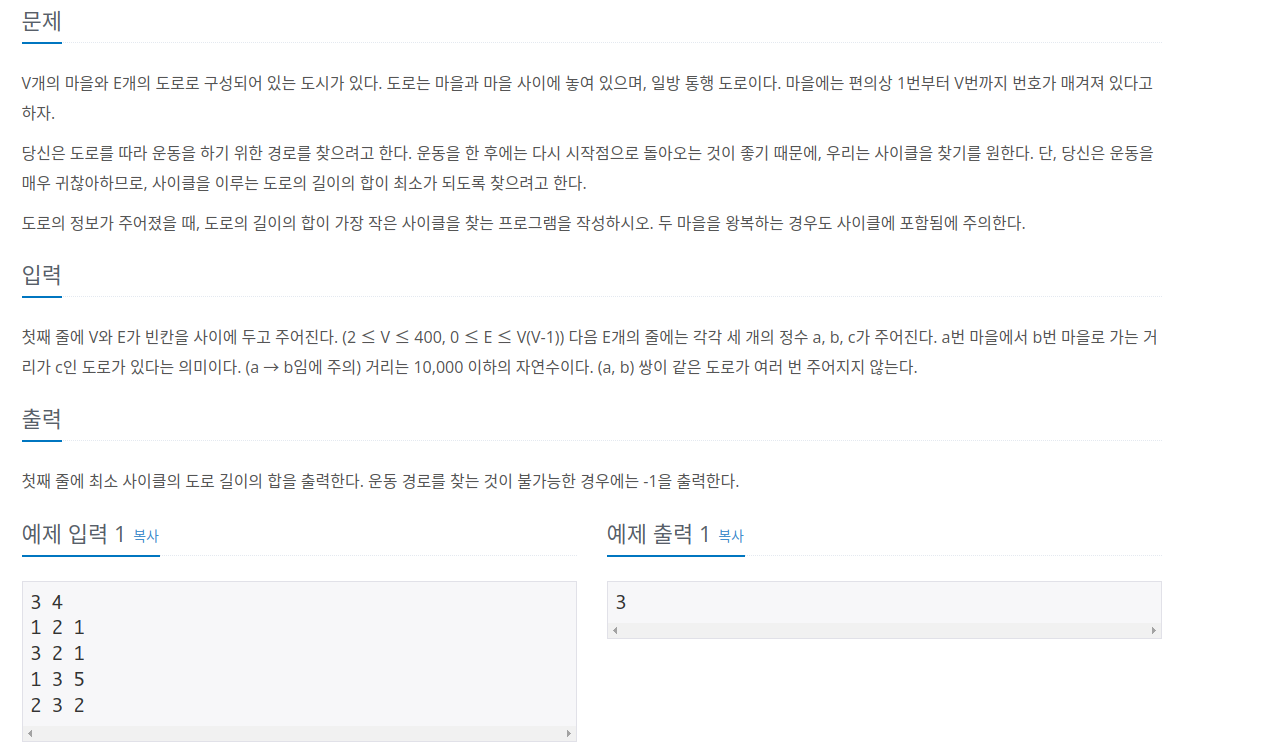
1956번: 운동

플로이드 와샬을 이용하면 쉽게 풀 수 있는 문제입니다.

플로이드 와샬 알고리즘을 모르시는 분은 해당 링크를 참고해주세요.

https://dongdd.tistory.com/10

Floyd-Warshall(플로이드 와샬) 알고리즘

 

문제에서 구하려는 것은 X -> X로 가려고 할 때, 거리의 최솟값을 구하는 문제였습니다.

2개 이상의 도로를 거쳐야 하기에 X -> X로 갈 때, 다른 정점을 거쳐야 했습니다.

 

따라서 플로이드 와샬 알고리즘을 이용해 j -> k로 갈 때 i라는 정점을 거쳐서 가는 것으로 j -> i + i -> k의 값을 얻는 것입니다.

 

해당 과정을 마치고, X -> X로 가는 방법 중, 최솟값을 가져오면 됐습니다.

 

 

자세한 것은 코드를 참고해주세요

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <vector>
#include <cstring>
#include <cmath>
#define P pair<int, int>
#define F first
#define S second
#define INF 987654321

using namespace std;

int N, M;
int Distance[401][401];

void reset_distance(){
    for(int i = 1; i <= N; i++){
        for(int j = 1; j <= N; j++){
            Distance[i][j] = INF;
        }
    }
}

void floyd_warshall(){
    for(int i = 1; i <= N; i++){ // i를 경유하여
        for(int j = 1; j <= N; j++){
            for(int k = 1; k <= N; k++){ j에서 k로 갈 때
                if(Distance[i][k] != INF && Distance[j][i] != INF){
                    Distance[j][k] = min(Distance[j][k], Distance[j][i] + Distance[i][k]);
                }
            }
        }
    }
}

void solve(){
    floyd_warshall();
    int mini = INF;
    for(int i = 1; i <= N; i++){
        mini = min(mini, Distance[i][i]);
    }
    if(mini == INF) cout << "-1";
    else cout << mini;
}

int main(){
    cin.tie(0);
    cout.tie(0);
    cin >> N >> M;
    reset_distance();
    for(int i = 1; i <= M; i++){
        int x, y, cost;
        cin >> x >> y >> cost;
        if(Distance[x][y] > cost) Distance[x][y] = cost;
    }
    solve();
    return 0;
}

 

 

질문 및 조언은 댓글을 남겨주세요