백준
백준 2042 - 구간 합 구하기(C++)
공대생의 잡다한 사전
2024. 3. 31. 21:39
문제 링크입니다. https://www.acmicpc.net/problem/2042
2042번: 구간 합 구하기
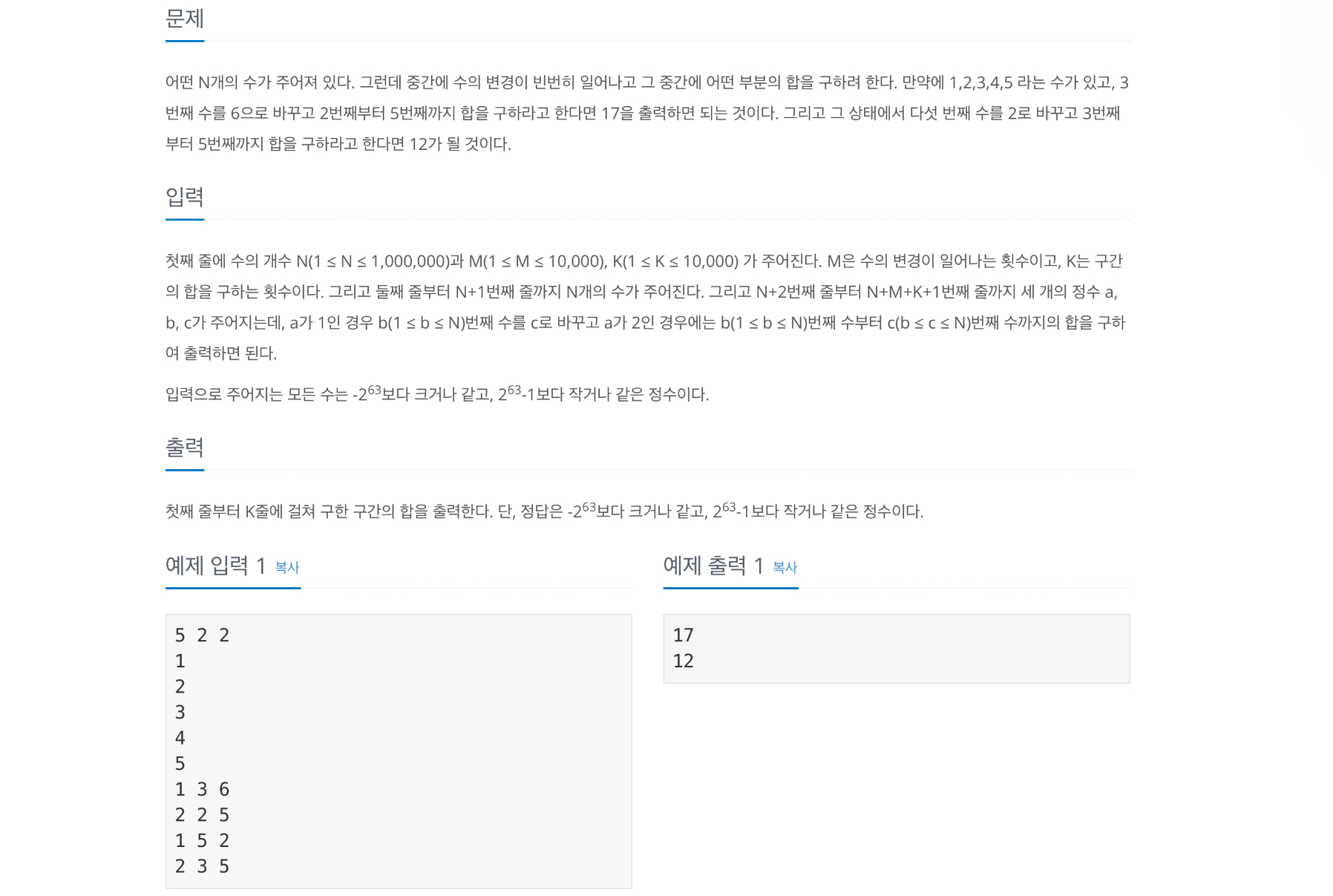
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄
www.acmicpc.net
세그먼트 트리를 사용하는 문제입니다.
세그먼트 트리에 대한 설명은 해당 블로그를 참고해주시길 바랍니다.
| https://yabmoons.tistory.com/m/431 |
자세한 것은 코드를 참고해주세요.
#define _CRT_SECURE_NO_WARNINGS
#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cmath>
#include <cstdio>
using namespace std;
int N, M, K;
int height;
long long index[1000001];
long long *Tree;
long long segment_tree(int node, int st, int fin){
if(st == fin) return Tree[node] = index[st];
int mid = (st + fin) / 2;
long long left_sum = segment_tree(node * 2, st, mid);
long long right_sum = segment_tree(node * 2 + 1, mid + 1, fin);
Tree[node] = left_sum + right_sum;
return Tree[node];
}
void change_tree(int node, int st, int fin, int loc, long long diff){
if(loc < st || loc > fin) return;
Tree[node] += diff;
if(st != fin){
int mid = (st + fin) / 2;
change_tree(node * 2, st, mid, loc, diff);
change_tree(node * 2 + 1, mid + 1, fin, loc, diff);
}
}
long long Sum_segment_tree(int node, int st, int fin, int left, int right){
if(left > fin || right < st) return 0;
if(left <= st && right >= fin) return Tree[node];
int mid = (st + fin) / 2;
long long left_sum = Sum_segment_tree(node * 2, st, mid, left, right);
long long right_sum = Sum_segment_tree(node * 2 + 1, mid + 1, fin, left, right);
return (left_sum + right_sum);
}
void solve(){
height = ceil(log2(N));
Tree = new long long[1 << (height + 1)];
segment_tree(1, 0, N - 1);
long long a, b, c;
for(int i = 1; i <= M + K; i++){
scanf("%lld %lld %lld", &a, &b, &c);
if(a == 1){ // 수를 바꿔라.
long long diff = c - index[b - 1];
index[b - 1] = c;
change_tree(1, 0, N - 1, b - 1, diff);
}
else{ // 주어진 구간의 합을 구하라.
cout << Sum_segment_tree(1, 0, N - 1, b - 1, c - 1) << "\n";
}
}
}
int main(){
cin.tie(0);
cout.tie(0);
cin >> N >> M >> K;
for(int i = 0; i < N; i++){
scanf("%lld", &index[i]);
}
solve();
return 0;
}

질문 및 조언은 댓글을 남겨주세요.