전자공학 및 알고리즘
백준 1753 - 최단경로(C++) 본문
문제 링크입니다. https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
다익스트라 알고리즘의 기본 문제입니다.


1. 다익스트라 알고리즘이란?
- 다익스트라 알고리즘은 그래프에서 최소 비용을 구해야 하는 경우 사용되는 알고리즘입니다.
최소 비용 중에서도, 주어진 두 노드(시작 노드, 도착 노드) 사이의 최소 비용인 경로를 찾을 때 사용됩니다.
2. 동작 원리
- 먼저 1차원 배열을 통해 X번 노드에서의 최소 값을 저장해야합니다. 해당 배열의 초기 값은 무한대로 저장되어 있습니다. 또한, 방문한 노드를 확인해야 하기에, 1차원 배열을 통해 방문 여부를 확인합니다.
- 1. 시작 노드와 직접 연결된 모든 정점들의 거리를 비교해 업데이트 하고, 시작 노드를 방문한 노드로 바꿔줍니다.
- 2. 방문한 정점들과 연결되어 있는 정점들 중, 비용이 가장 적게 드는 정점을 확인합니다. (이때 방문할 점이 이전에 탐색한 점이 아니여야됩니다.)
- 3. 비용이 가장 적은 노드를 확인했다면, 해당 정점을 방문했다고 바꿔주고, 해당 정점에서 연결된 정점들을 확인합니다.
- 4. 2~3번 과정을 반복합니다.
해당 과정을 그림을 통해 확인해겠습니다.

해당 그래프가 있다고 하겠습니다. 시작 노드는 '1번'이라고 하겠습니다.
모든 정점이 최소 길이가 무한, 이전에 방문하지 않았다고 저장되어 있는 상태입니다.
1. 시작 노드와 직접 연결된 모든 정점들의 거리를 비교해 업데이트 하고, 시작 노드를 방문한 노드로 바꿔줍니다.
- 시작 노드와 연결된 노드는 2번과 3번입니다. 각각 비용이 4, 5이니 해당 노드에서 최소 거리를 바꿔줍니다.
1번 정점을 확인했으니, 방문한 정점으로 바꿔줍니다. 이때, 자기 자신을 방문할 때 비용은 0이니, 비용도 바꿔줍니다.
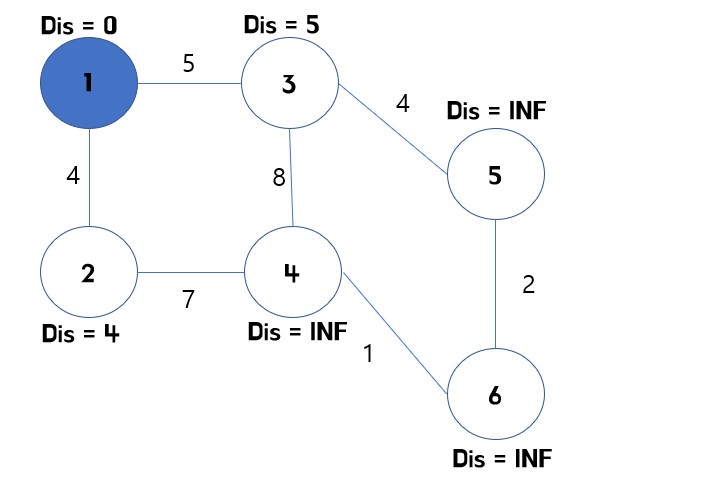
2 + 3.방문한 정점들과 연결되어 있는 정점들 중, 비용이 가장 적게 드는 정점을 확인하고 해당 정점을 방문했다고 바꿔준뒤, 해당 정점에서 연결된 정점들을 확인합니다.
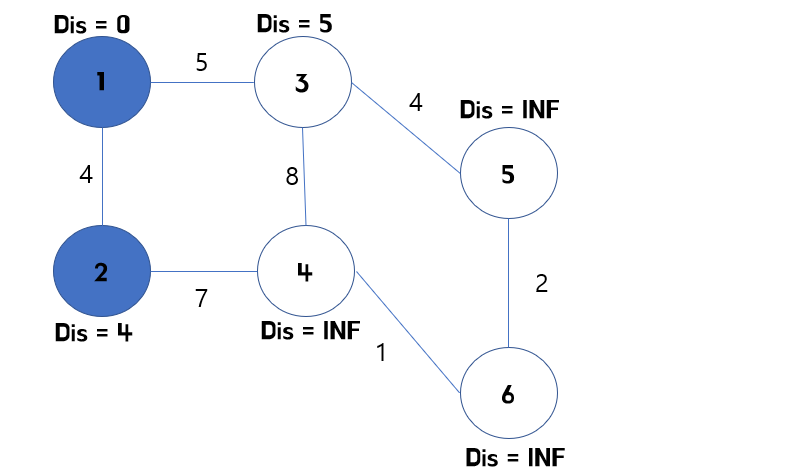
- 1번 정점에서 가장 비용이 적은 정점은 2번입니다. 따라서 2번 정점을 방문했다는 표시를 해주고 해당 점에서 연결된 4번 점을 확인합니다.
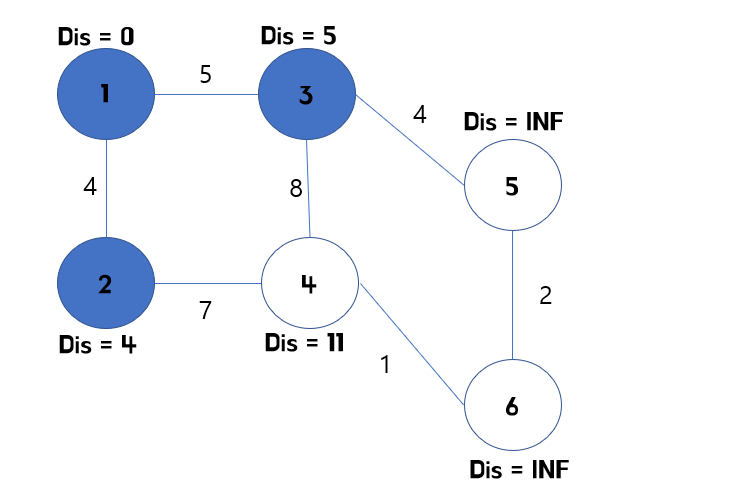
2번 점을 확인했다면, 이제 3번 정점을 확인해야합니다. 따라서 3번 정점에서 연결된 정점인 5번을 확인해주고, 5번의 최소 비용을 바꿔줍니다.
이때, 5번의 최소 비용이 4번의 최소 비용보다 작으니, 5번 부터 확인해줍니다.
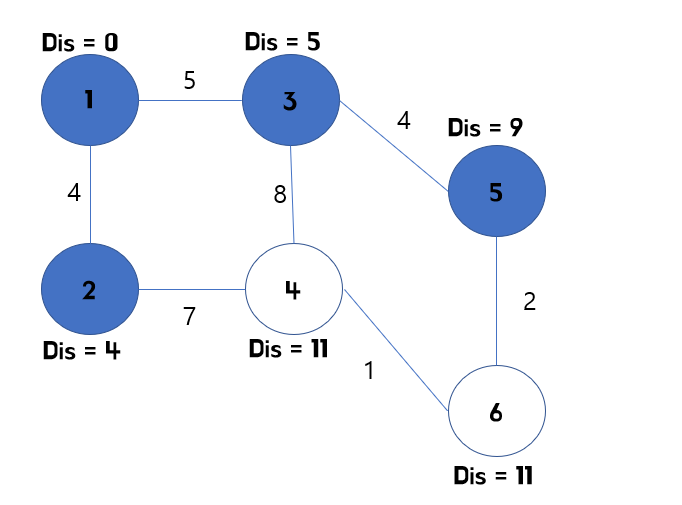

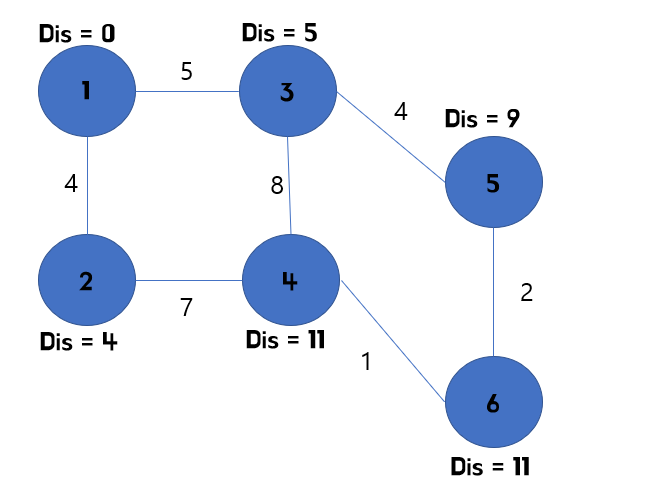
해당 과정에서 생길 수 있는 의문이 있습니다.
다른 경로로 갔을 때가 더 작은 비용이라면?? -> 우선 순위 큐로 관리하기에 해당 의문이 해결될 수 있습니다.
위의 설명을 이해하셨다면, 해당 문제도 풀 수 있습니다.
먼저 시작점과 간선의 정보가 주어집니다.
간선의 정보는 vector를 통해 저장하고, 1차원 배열 2개를 이용해, 정점의 방문 여부, 최소 비용을 저장해줍니다.
long long int Distance[20001];
bool check[200001];
vector<pair<int, int>> connect[200001];
우선 순위 큐를 오름 차순으로 정렬될 수 있도록 선언해 줍니다.
priority_queue<pair<long long int, int>, vector<pair<long long int, int>>, greater<pair<long long int, int>>> q;
X점에서 시작한다고 했을 때, vector에 저장된 정보를 통해 X점에서 연결된 정점으로 갈 수 있는 최소 비용을 확인합니다. 이때 최소 비용을 바꿀 정점은 이전에 방문하지 않았던 점이여야 합니다.
최소 비용을 구했다면, 해당 정점을 우선 순위 큐에 넣어줍니다.
while (!q.empty()) {
int x = q.top().second;
int cost = q.top().first;
q.pop();
check[x] = true;
for (int i = 0; i < connect[x].size(); i++) {
int xx = connect[x][i].first;
int Cost = connect[x][i].second;
if (!check[xx] && Distance[xx] > Distance[x] + Cost) {
Distance[xx] = Distance[x] + Cost;
q.push(make_pair(Distance[xx], xx));
}
}
}
자세한 것은 코드를 참고해주세요
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <cstring>
#include <string>
#include <queue>
#include <stack>
#include <cmath>
#define INF 210000000000
using namespace std;
priority_queue<pair<long long int, int>, vector<pair<long long int, int>>, greater<pair<long long int, int>>> q;
int N, M;
int start;
long long int Distance[20001];
bool check[200001];
vector<pair<int, int>> connect[200001];
void reset_Distance() {
for (int i = 1; i <= N; i++) {
Distance[i] = INF;
}
}
void solve() {
reset_Distance();
memset(check, false, sizeof(check));
Distance[start] = 0;
q.push(make_pair(Distance[start], start));
while (!q.empty()) {
int x = q.top().second;
int cost = q.top().first;
q.pop();
check[x] = true;
for (int i = 0; i < connect[x].size(); i++) {
int xx = connect[x][i].first;
int Cost = connect[x][i].second;
if (!check[xx] && Distance[xx] > Distance[x] + Cost) {
Distance[xx] = Distance[x] + Cost;
q.push(make_pair(Distance[xx], xx));
}
}
}
for (int i = 1; i <= N; i++) {
if (Distance[i] != INF) {
cout << Distance[i] << "\n";
}
else cout << "INF" << "\n";
}
}
int main()
{
cin.tie(0);
cout.tie(0);
cin >> N >> M;
cin >> start;
for (int i = 1; i <= M; i++) {
int x, y, cost;
cin >> x >> y >> cost;
connect[x].push_back(make_pair(y, cost));
}
solve();
return 0;
}

질문 및 조언 댓글 남겨주세요
'백준' 카테고리의 다른 글
| 백준 1504 - 특정한 최단 경로(C++) (0) | 2022.03.09 |
|---|---|
| 백준 1916 - 최소비용 구하기(C++) (0) | 2022.03.07 |
| 백준 1865 - 웜홀(C++) (0) | 2022.03.06 |
| 백준 2407 - 조합(C++) (0) | 2022.02.25 |
| 백준 11404 - 플로이드(복습, C++) (0) | 2022.02.25 |




