Notice
Recent Posts
Recent Comments
Link
전자공학 및 알고리즘
백준 18223 - 민준이와 마산 그리고 건우(C++) 본문
문제 링크입니다. https://www.acmicpc.net/problem/18223
18223번: 민준이와 마산 그리고 건우
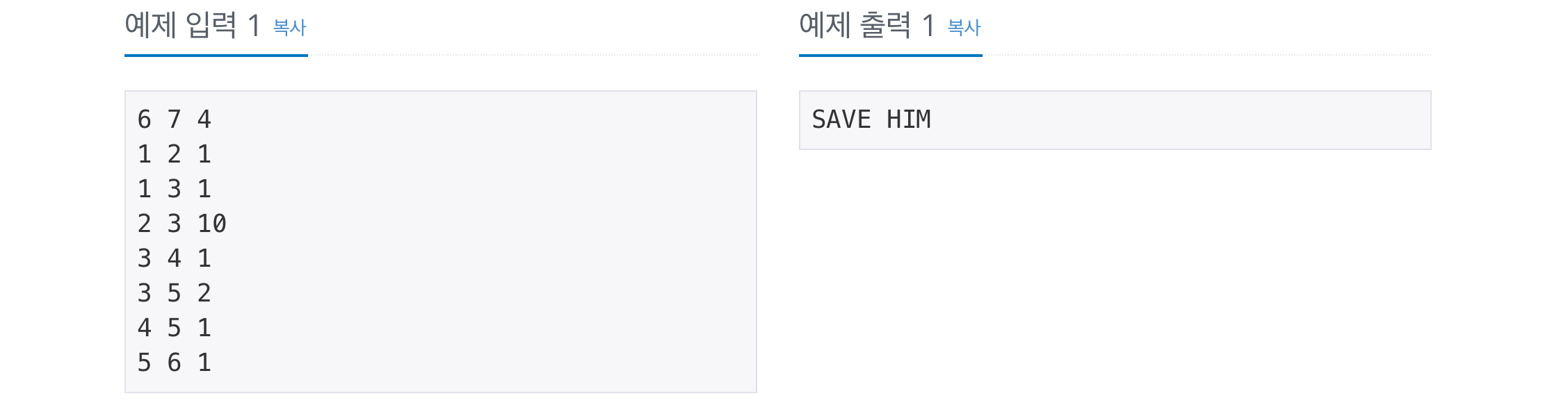
입력의 첫 번째 줄에 정점의 개수 V와 간선의 개수 E, 그리고 건우가 위치한 정점 P가 주어진다. (2 ≤ V ≤ 5,000, 1 ≤ E ≤ 10,000, 1 ≤ P ≤ V) 두 번째 줄부터 E개의 줄에 걸쳐 각 간선의 정보
www.acmicpc.net
다익스트라 알고리즘을 활용한 문제입니다.
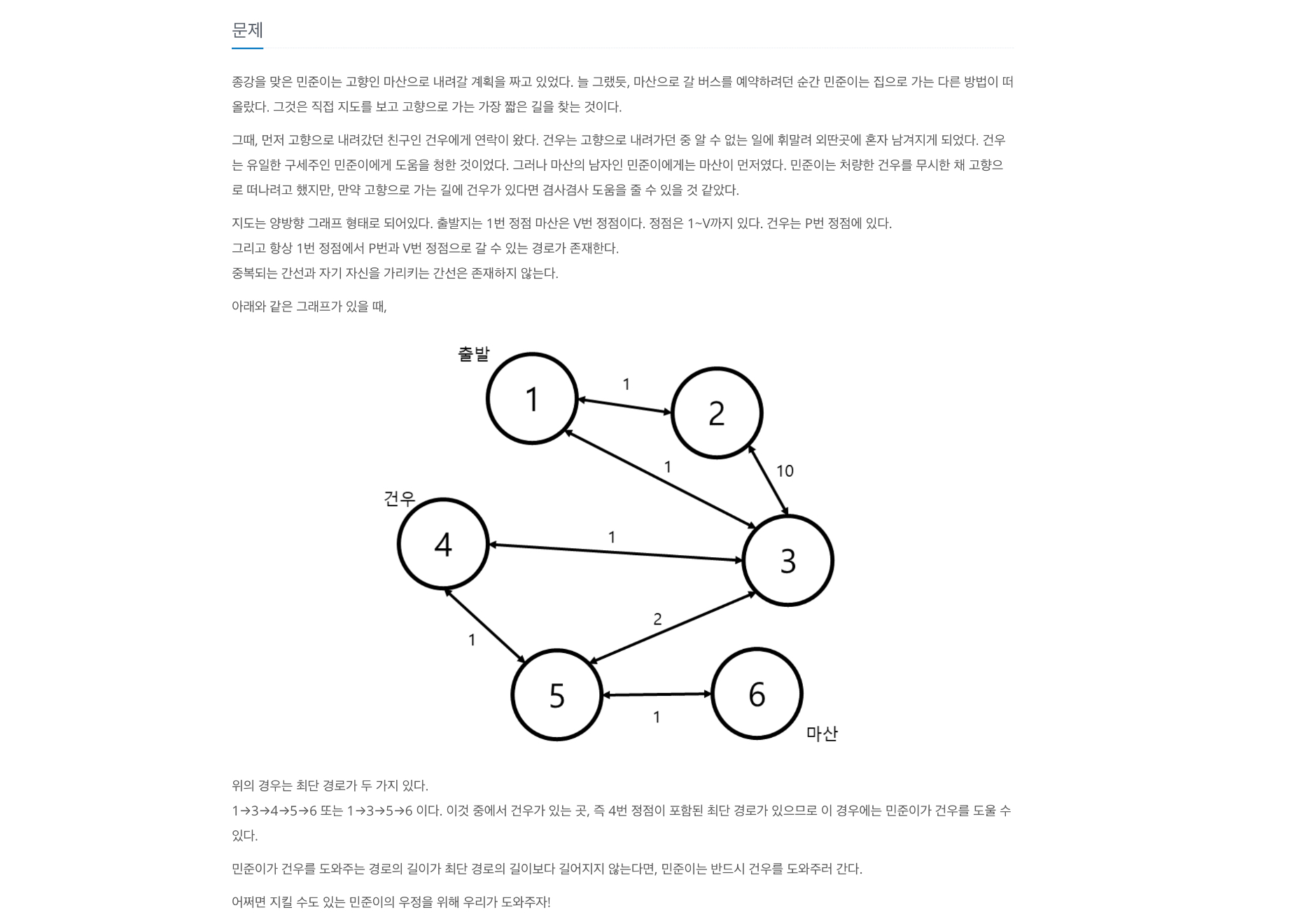
문제를 풀기 위해선
1->N 점까지 가는 최단 거리가 1->민준->N 점으로 가는 최단거리와 같은 것인지를 알아야 했습니다.
->이 두 경우의 값이 같다면 항상 민준이는 건우를 도울 수 있기 때문입니다.
따라서 1->N까지 가는 다익스트라로 원래 최단 거리를,
1->민준 + 민준->N의 최단 거리의 합을 구해 두 경우가 같은지를 확인해줬습니다.
자세한 것은 코드를 참고해주세요.
#define _CRT_SECURE_NO_WARNINGS
#include <cstring>
#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cmath>
#include <cstdio>
#include <string>
#define INF 2100000000
#define F first
#define S second
using namespace std;
int p, v, e;
priority_queue<pair<int, int>, vector<pair<int, int>>> q;
int Distance[5001];
int visit_p[5001];
vector<pair<int, int>> connect[5001];
void reset_distance(){
for(int i = 1; i <= v; i++) Distance[i] = INF;
}
int dijstra(int st, int fin){
reset_distance();
Distance[st] = 0;
q.push({-0, st});
while(!q.empty()){
int x = q.top().S;
int cost = -q.top().F;
q.pop();
for(int i = 0; i < connect[x].size(); i++){
int xx = connect[x][i].F;
int n_cost = connect[x][i].S + cost;
if(Distance[xx] > n_cost){
Distance[xx] = n_cost;
q.push({-Distance[xx], xx});
}
}
}
return Distance[fin];
}
void solve(){
int min_cost = dijstra(1, v);
int p_cost = dijstra(1, p) + dijstra(p, v);
if(min_cost == p_cost) cout << "SAVE HIM";
else cout << "GOOD BYE";
}
int main() {
cin.tie(0);
cout.tie(0);
cin >> v >> e >> p;
for(int i = 1; i <= e; i++){
int x, y, cost;
cin >> x >> y >> cost;
connect[x].push_back({y, cost});
connect[y].push_back({x, cost});
}
solve();
return 0;
}
질문 및 조언은 댓글을 남겨주세요.
'백준' 카테고리의 다른 글
| 백준 20007 - 떡 돌리기(C++) (1) | 2023.11.27 |
|---|---|
| 백준 23793 - 두 단계 최단 경로 1(C++) (1) | 2023.11.24 |
| 백준 13424 - 비밀 모임(C++) (1) | 2023.11.20 |
| 백준 13398 - 연속합 2(C++) (1) | 2023.11.20 |
| 백준 14284 - 간선 이어가기 2(C++) (0) | 2023.11.15 |




