전자공학 및 알고리즘
백준 4792 - 레드 블루 스패닝 트리(C++) 본문
문제 링크입니다. https://www.acmicpc.net/problem/4792
4792번: 레드 블루 스패닝 트리
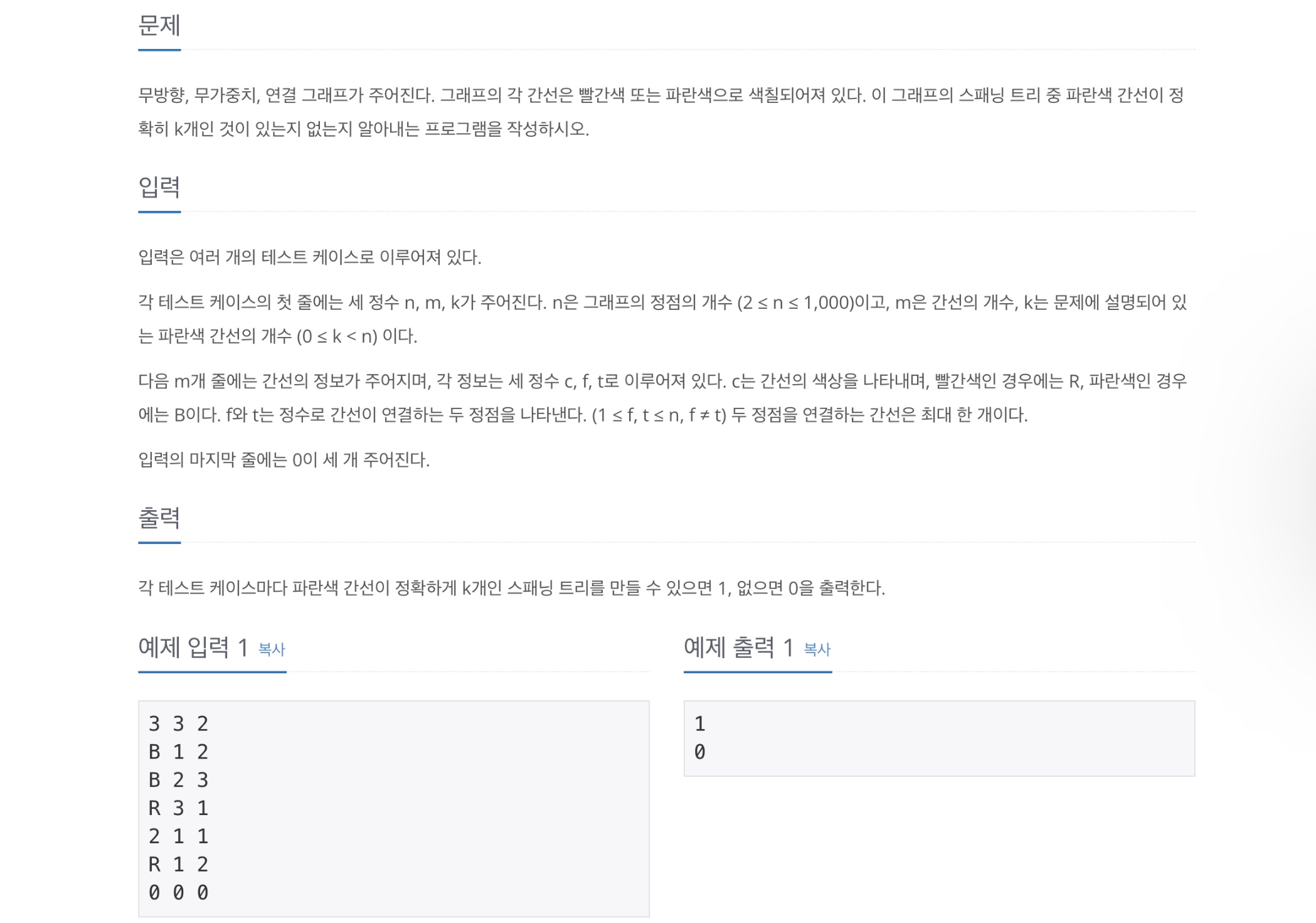
무방향, 무가중치, 연결 그래프가 주어진다. 그래프의 각 간선은 빨간색 또는 파란색으로 색칠되어져 있다. 이 그래프의 스패닝 트리 중 파란색 간선이 정확히 k개인 것이 있는지 없는지 알아내
www.acmicpc.net
간단한 것 같으면서도 풀 방법이 쉽게 떠오르지 않는 문제였습니다.
주어진 파란색 간선 중, 최소 스패닝 트리를 구현하기 위해서 무조건 사용해야 하는 간선이 존재할 수 있습니다.
그러한 간선이 몇 개인지를 찾기 위해서 빨간색 간선을 오름차순 기준으로 만들어 정렬을 해준 뒤, 최소 스패닝 트리를 사용해주면 됩니다.
이때, 쉽게 구현하기 위해서 파란색 간선에는 1의 가중치, 빨간색 간선에는 0의 가중치를 부여했습니다.
그렇다면, 잉여의 파란색 간선이 남았다면 이들을 빨간색 간선을 대체 할 수 있는지를 생각해봐야 할 것입니다.
한번 생각을 해보겠습니다.
예를 들어, 추가할 파란색 간선이 X -> Y라고 하겠습니다.
그렇다면 기존에 X -> Y 간선을 가기 위한 길 중, 하나의 간선을 제거하고 파랑색 간선을 추가한다면 문제없이 그래프가 연결될 것입니다.
(기존의 간선들을 모두 제거한다면 당연하게도 최소 스패닝 트리가 성립되지 않습니다)
하지만, 기존에 연결된 X -> Y 간선들이 오로지 파란색 간선들 만으로 이용되어 있다면? -> 해당 경우는 사용된 파란색 간선의 갯수는 그대로가 됩니다.
그렇지만, 기존에 연결된 X -> Y 간선들 중, 빨간색 간선이 한개라도 있다면? -> 사용된 파란색 간선이 한개가 늘어납니다.
이런 방법을 통해 몇개까지 파란색 간선을 사용할 수 있는지 확인하는 것을 어려우니, 애초에 사용된 파란색 간선의 갯수의 최댓값을 구하면 됩니다.
그렇다면, 사용된 파랑색 그래프의 최댓값과 최솟값 사이에 K의 값이 존재한다면 이는 만들 수 있는 그래프가 될 것입니다.
자세한 것은 코드를 참고해주세요.
#define _CRT_SECURE_NO_WARNINGS
#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cmath>
#include <cstdio>
#include <cstring>
using namespace std;
int N, M, K;
typedef struct info{
int x;
int y;
int cost;
}info;
vector<info> connect;
int parent[1001];
void reset_parent(){
for(int i = 1; i <= N; i++){
parent[i] = i;
}
}
bool cmp_1(info a, info b){ // R간선을 오름차순
if(a.cost < b.cost) return true;
else return false;
}
bool cmp_2(info a, info b){ // B간선을 오름차순
if(a.cost > b.cost) return true;
else return false;
}
void Union(int x, int y){
if(x < y) parent[x] = y;
else parent[y] = x;
}
int Find(int x){
if(x == parent[x]) return x;
else return parent[x] = Find(parent[x]);
}
void solve(){
int min_use = 0, max_use = 0;
///////////// B 간선을 최소로 사용할 경우
reset_parent();
sort(connect.begin(), connect.end(), cmp_1);
for(int i = 0; i < connect.size(); i++){
int x = Find(connect[i].x);
int y = Find(connect[i].y);
if(x != y){
Union(x, y);
min_use += connect[i].cost;
}
}
//////////// B 간선을 최대로 사용할 경우
reset_parent();
sort(connect.begin(), connect.end(), cmp_2);
for(int i = 0; i < connect.size(); i++){
int x = Find(connect[i].x);
int y = Find(connect[i].y);
if(x != y){
Union(x, y);
max_use += connect[i].cost;
}
}
if(K >= min_use && K <= max_use) cout << "1" << "\n";
else cout << "0" << "\n";
}
int main(){
cin.tie(0);
cout.tie(0);
while(1){
scanf("%d %d %d", &N, &M, &K);
if(N == 0 && M == 0 && K == 0) break;
connect.clear();
for(int i = 1; i <= M; i++){
int x, y;
char cost;
cin >> cost >> x >> y;
if(cost == 'R') connect.push_back({x, y, 0});
else connect.push_back({x, y, 1});
}
solve();
}
return 0;
}
질문 및 조언은 댓글을 남겨주세요.
'백준' 카테고리의 다른 글
| 백준 9420 - Strahler 순서(C++) (1) | 2024.03.11 |
|---|---|
| 백준 2637 - 장난감 조립(C++) (0) | 2024.03.08 |
| 백준 1185 - 유럽여행(C++) (0) | 2024.02.25 |
| 백준 1833 - 고속철도 설계하기(C++) (0) | 2024.02.22 |
| 백준 23034 - 조별과제 멈춰!(C++) (0) | 2024.02.21 |




