알고리즘 모음(C++)
백준 2357 - 최솟값과 최댓값(C++) 본문
문제 링크입니다. https://www.acmicpc.net/problem/2357
2357번: 최솟값과 최댓값
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수, 또는 제일 큰 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100
www.acmicpc.net
세그먼트 트리를 이용해 푸는 문제입니다.
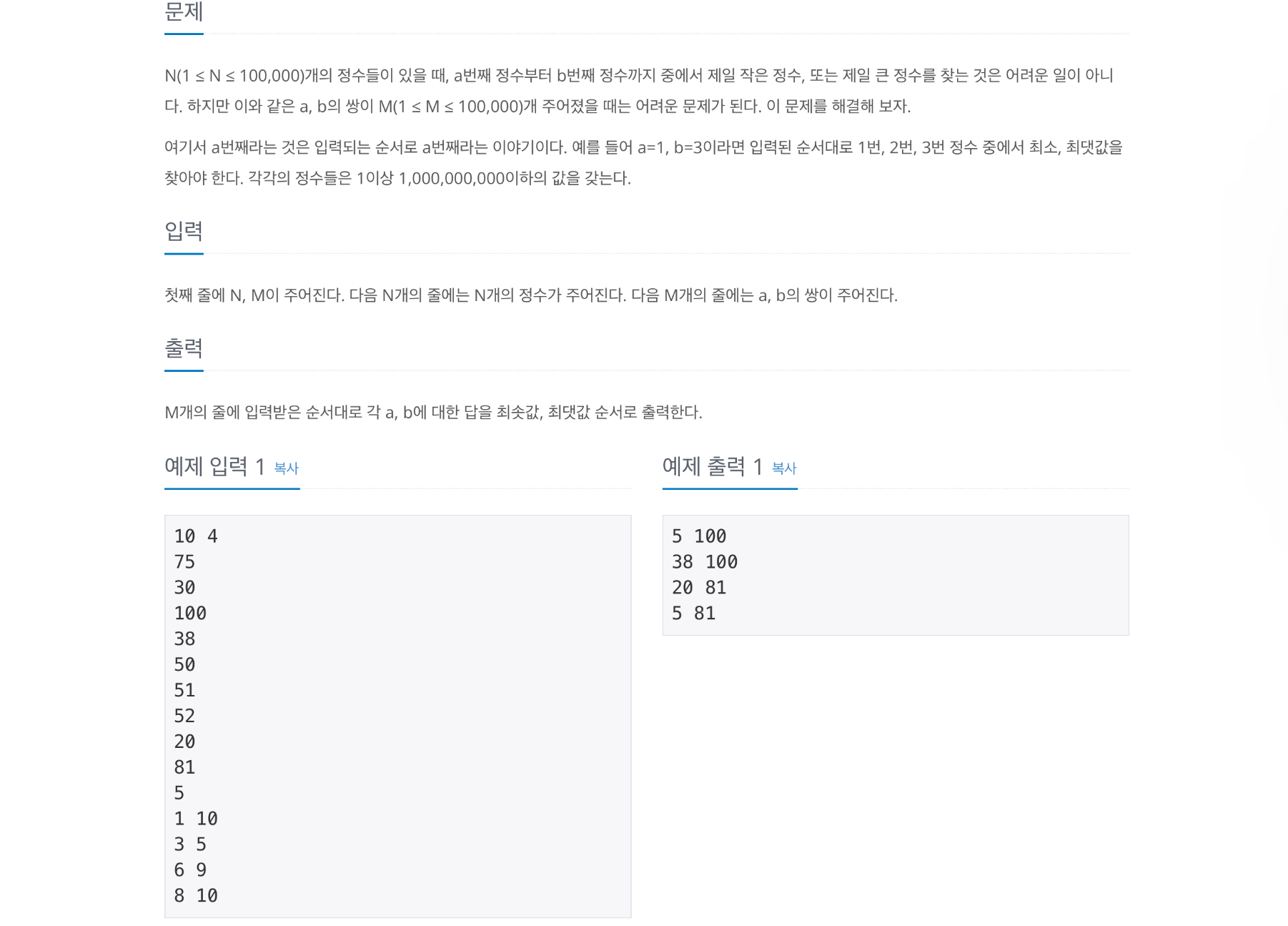
주어진 N개의 값이 있을 때, M개만큼 (a, b)의 쌍이 주어집니다.
이때, (a, b) 범위 안의 값의 최솟값과 최댓값을 구하는 문제입니다.
N, M의 범위가 100,000까지 이기에 단순히 탐색을 한다면 시간 초과가 생길 것입니다.
따라서, 세그먼트 트리를 이용해 탐색 횟수를 줄여 답을 구할 것입니다.
하지만, 일반적인 트리를 구한 뒤, 탐색을 한다면, 일반적인 탐색과 다른 것이 없습니다.
저는 트리를 구할 때, 최솟값과 최댓값을 같이 저장하는 트리를 만들어서 저장해줬습니다.
최솟값이나 최댓값을 구할 때,
1. 구하려는 범위가 현재 시작점과 끝점의 범위에 속하지 않는 경우
-> 해당 범위는 벗어났음으로 탐색하지 않는다,
2. 구하려는 범위 안이 시작점과 끝점이 속할 경우
-> 해당 범위의 최솟값과 최댓값은 이미 구해져 있기에 해당 값을 쓴다,
3. 구하려는 범위와 시작점과 끝점이 결쳐 있는 경우
-> 왼쪽, 오른쪽 자식을 탐색하면서 정확한 범위를 찾아 구한다.
해당 방식으로 트리를 탐색해 구해주면 됩니다.
자세한 것은 코드를 참고해주세요.
#define _CRT_SECURE_NO_WARNINGS
#include <vector>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cmath>
#include <cstdio>
#include <climits>
using namespace std;
int N, M;
int index[100001];
vector<long long> Tree;
vector<int> Min_tree;
vector<int> Max_tree;
long long segment_tree(int node, int st, int fin){
if(st == fin) {
Min_tree[node] = index[st];
Max_tree[node] = index[st];
return Tree[node] = index[st];
}
int mid = (st + fin) / 2;
long long left_sum = segment_tree(node * 2, st, mid);
long long right_sum = segment_tree(node * 2 + 1, mid + 1, fin);
Max_tree[node] = max(Max_tree[node * 2], Max_tree[node * 2 + 1]);
Min_tree[node] = min(Min_tree[node * 2], Min_tree[node * 2 + 1]);
return Tree[node] = (left_sum + right_sum);
}
int check_tree(int node, int st, int fin, int left, int right, bool Type){
if(left > fin || right < st){
if(!Type) return INT_MAX; //작은 값을 구할 떄
else return -INT_MAX; //큰 값을 구할 때
}
if(left <= st && right >= fin){
if(!Type) return Min_tree[node];
else return Max_tree[node];
}
int mid = (st + fin) / 2;
int left_value = check_tree(node * 2, st, mid, left, right, Type);
int right_value = check_tree(node * 2 + 1, mid + 1, fin, left, right, Type);
if(!Type) return min(left_value, right_value);
else return max(left_value, right_value);
}
void solve(){
int height = ceil(log2(N));
int tree_height = 1 << (height + 1); Tree.resize(tree_height);
Max_tree.resize(tree_height);
Min_tree.resize(tree_height);
segment_tree(1, 0, N - 1);
for(int i = 1; i <= M; i++){
int x, y;
scanf("%d %d", &x, &y);
cout << check_tree(1, 0, N - 1, x - 1, y - 1, false);
cout << " ";
cout << check_tree(1, 0, N - 1, x - 1, y - 1, true);
cout << "\n";
}
}
int main(){
cin.tie(0);
cout.tie(0);
cin >> N >> M;
for(int i = 0; i < N; i++){
scanf("%d", &index[i]);
}
solve();
return 0;
}

질문 및 조언은 댓글을 남겨주세요.
'백준' 카테고리의 다른 글
| 백준 11505 - 구간 곱 곱하기(C++) (0) | 2024.05.03 |
|---|---|
| 백준 10868 - 최솟값(C++) (1) | 2024.04.02 |
| 백준 2042 - 구간 합 구하기(C++) (0) | 2024.03.31 |
| 백준 14567 - 선수과목 (Prerequisite)(C++) (1) | 2024.03.26 |
| 백준 2152 - 여행 계획 세우기(C++) (2) | 2024.03.24 |




