전자공학 및 알고리즘
전기자기학 1장 - vector + 좌표계 본문

해당 페이지에서는 vector의 성질에 대해서 알아봤습니다.
여기서는 결합 법칙과 분배 법칙을 기억해주시면 될거 같습니다.

vector의 dot product, cross product에 관한 내용과 데카르트 좌표계에 대한 내용입니다.
dot prouct는 내적이라고 불리며 cross product는 외적이라고 불립니다.
내적의 결과는 스칼라 값이며 외적은 vector 값이라는 것은 기억해줘야 합니다.
내적과 외적의 식도 기억해야 합니다.
데카르트 좌표계는 X,Y,Z를 사용하는 좌표계입니다.

먼저 vector의 표현과 관련된 내용입니다.
백터의 크기를 구하는 방법, 해당 방향의 백터를 단위백터로 만드는 방법을 알아두시면 됩니다.
다음은 해당 좌표계에서 내적과 외적을 사용할 때 나오는 결과에 대한 내용입니다.
Dot product 의 경우, 같은 방향의 vector만 결과가 값이 나오는 것을 볼수 있습니다. ( Ex) X, X가 내적될 경우에만 값이 나온다 )
Cross product의 경우는 3*3 행렬 연산과 같은 결과가 나온다는 것만 알아두시면 됩니다.
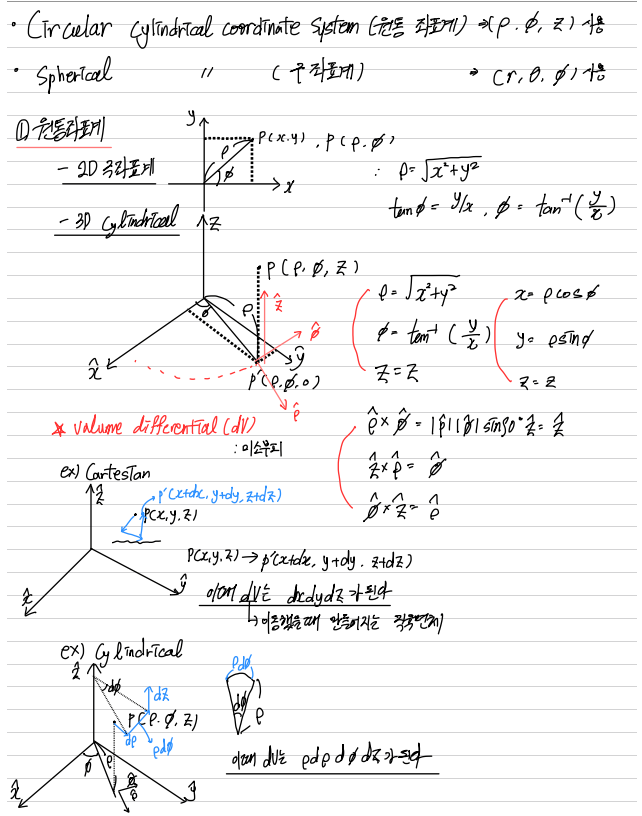
이제는 구와 원기둥 좌표계를 알아보겠습니다.
먼저 두 좌표계에서 사용하는 기호에 익숙해져야합니다. 뒷장에 갈 수록 두 좌표계가 많이 사용됩니다.
해당 페이지에서 가장 중요한 내용은 dV를 구하는 방법입니다.
먼저 Cartesian 좌표계에서는 부피의 변화율이 x, y, z좌표의 이동값의 곱입니다. 따라서 dxdydz로 쉽게 구할수 있습니다.
하지만 원기둥 좌표계에서는 dV가 다르게 나옵니다. 움직인 각도를 생각해야하기 때문인데, 움직인 부채꼴의 호의 길이는 움직인 각도에 ℓ가 곱해져야 합니다. 따라서 dV가 해당 수식처럼 나오게 됩니다.

Cartesian좌표계로 나타낸 백터를 원기둥 좌표계로 바꾸는 내용이 중요합니다.
바꾸는 방법은 원기둥 좌표에서 사용하는 기호를 단위백터로 곱해주면 됩니다.
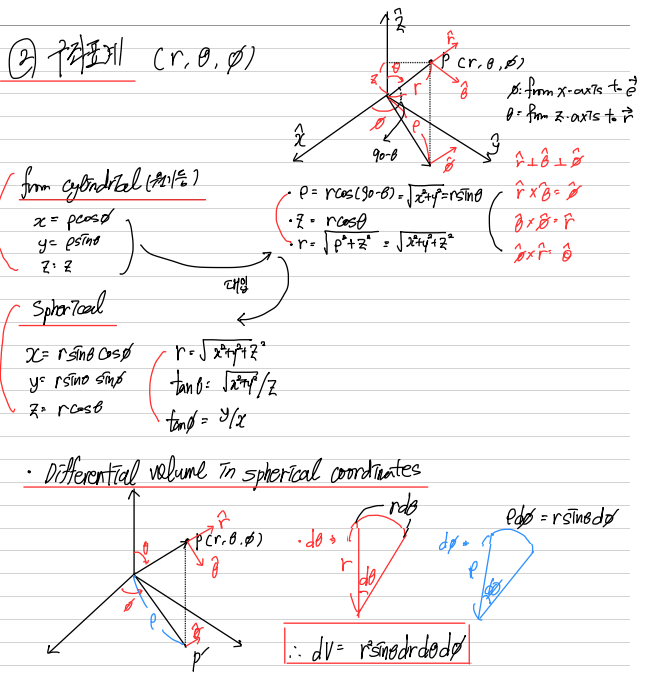
이번에는 구 좌표계와 관련된 내용입니다.
표현 방법과 dV를 구하는 방법은 원기둥 좌표계와 비슷하니 이해하기 쉽습니다.
전기자기학 1장 내용입니다.
백터의 표현과 법칙 그리고 다양한 좌표계에 대해서 알아봤습니다.
1단원의 내용은 앞으로의 기본이 됨으로 확실하게 알아두셔야 합니다.
특히 dV와 관련해서 나타나는 표현을 확실히 이해해야합니다.
질문 및 오류는 댓글 남겨주세요.
'전기자기학' 카테고리의 다른 글
| 전기자기학 3장 - 전속 밀도, 가우스 법칙, 맥스웰 방정식, Divergence(1) (0) | 2022.07.07 |
|---|---|
| 전기자기학 2장 - 연습문제 풀이 (0) | 2022.05.17 |
| 전기자기학 2장 - 전하와 쿨롱 법칙, 밀도 (0) | 2022.05.08 |
| 전기자기학 1장 - 연습문제 풀이 (0) | 2022.05.08 |
| 전기자기학 시작 전 (0) | 2022.05.08 |




