전자공학 및 알고리즘
Unit 1 - Binary Number(part 1) 본문
Analog circuits 과 Digital circuits 의 차이점
Analog circuits
- 전자 시스템이 연속적으로 변하는 신호를 가지고 있다.
- 신호는 주어진 범위에서 임의의 값을 가진다.
- 아날로그 시스템은 항상 무작위적 변형과 교란인 노이즈를 포함한다
- 아날로그 회로는 디자인하기 허려워서 디지털 신호보다 더 많은 숙련도를 요구한다.
Digital circuits
- 디지털 신호는 연속적인 범위(아날로그에서 사용)보다는 분리된 아날로그 범위를 사용한다.
- 같은 범위 안에 있는 값은 같은 값을 나타낸다.
- 2개의 값으로 표시된다. GND - 0V , 다른 값은 전원이 공급된다. false -> 0, true -> 1
- 디지털로 표현된 신호는 noise 때문에 품질저하 없이 이동할 수 있다.
- 더 많은 이진수를 사용함으로써 신호의 더 정확한 표현을 얻을 수 있습니다.
- Computer - controlled 디지털 신호는 소프트웨어로 작동하기에 하드웨어의 추가 없이 더 많은 기능을 사용할 수 있습니다.
- 아날로그에서 디지털의 전환은 작은 양의 error를 생산합니다. (quantization error)
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
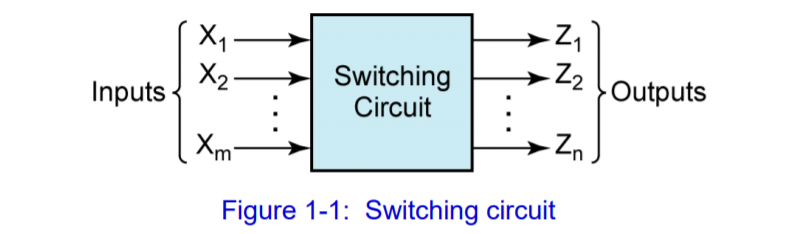
Swiching Circuit
1. Combinational circuit(조합회로)
결과값이 오로지 현재 입력된 값에 의해서 결정된다.
2. Sequential circuit
결과값이 현재, 과거에 입력된 값에 의해 결정된다 -> memory를 가지고있다.
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Binary Number
- 0과 1의 두 값을 가집니다.
- 각각의 수는 "bit"라고 불립니다.
Good things in binary number
- 수가 오로지 0과 1의 값으로 표현됩니다.
- 간단한 전자 장치로 구현이 가능하다. (Voltage high ->1, low -> 0 / Switch on -> 1, off -> 0)
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Number Systems and Conversion
1. Positional notation(위치 표기법)
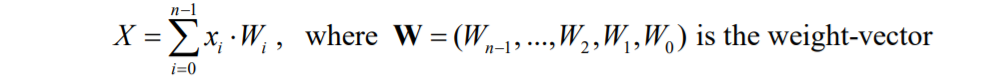
ex) 953.78(10진수) = 9 * 10^2 + 5 * 10^1 + 3 * 10^0 + 7 * 10^-1 + 8 * 10^-2
1011.11(2진수) = 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 + 1 * 2^-1 + 1 * 2^-2
= 8 + 2 + 1 + 0.5 + 0.25 = 11.75
이때 10과 2를 W(Weight)이라고 한다.
- 로마숫자, 正와 같은 수는 위치 표기법이 아니다.
2. Radix number system
각 자릿수에서 표현할 수 있는 종류의 갯수를 Radix라고 한다.(10진수 -> 0 ~ 9 , 2진수 -> 0~1)
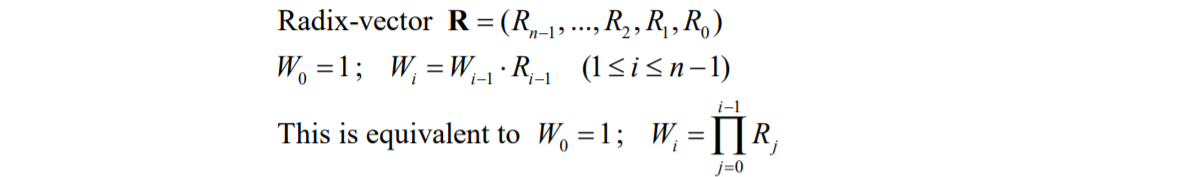
- Fixed-radix system -> 모든 자릿수가 같은 radix를 의미한다.
- Mixed-radix system -> 자릿수가 같은 radix가 아닌 것을 의미한다.(ex) 시간 -> (24시, 60분, 60초) -> R = (24,69,60) , W = (3600, 60 , 1) 이 된다.
3. General form of a fixed-radix number

- Radix point = 소수점 -> Radix point를 기준으로 왼쪽을 integer part, 오른쪽을 fractional part라고 한다.
- 가장 왼쪽을 most significant digit(bit), 가장 왼쪽을 least significant digit(bit)이라고 한다. bit - binary의 경우
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
1. 위치 표기법으로 쓰여진 숫자는 power series in R 로 확장 가능합니다.
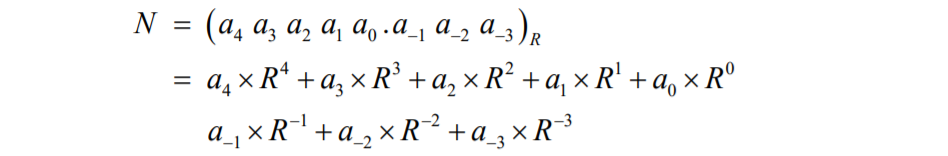

2. power series in R 확장을 사용하여 모든 base로 변환할 수 있습니다.
ex) 10 - > 3 or 10 - > 2
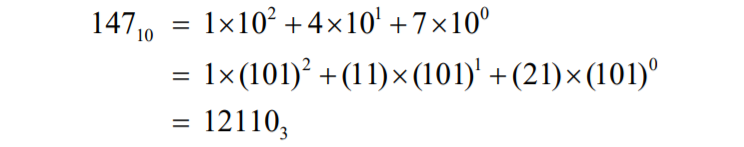

3. 10이상의 진법의 표현
-> 11 -> A, 12 -> B, 13 -> C, 14 -> D..........
16진수 -> 2진수, 2진수 -> 16진수 변환 방법


4자리로 끊은 이유 -> 2진수로 0~15까지 4자리로 나타내기 때문
4. 나누기로 R1 -> R2로 변환하는 방법(나머지 사용)(integer part)
ex) 55(10)을 2진수로 바꾸기
55/2 = 27 ... 1
27/2 = 13 ... 1
............. -> 110111
55(10)을 8진수로 바꾸기
55/8 = 6 ... 7
6/8 = 0 ... 6 -> 67
55(10)을 16진수로 바꾸기
55/16 = 3 ... 7
3/16 = 0 ... 3 -> 37
5. 곱하기를 사용해서 R1 -> R2로 변환하는 방법(fraction part)
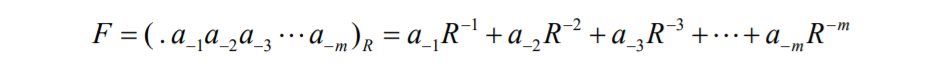
위와 같이 fraction part가 있을 때, R을 계속 곱해준다.


6. 두개의 bases 간의 변환은 R1 -> 10 -> R2로 바꾸는 것이 편하다. 이때 integer, fraction part를 나눠서 구한다.
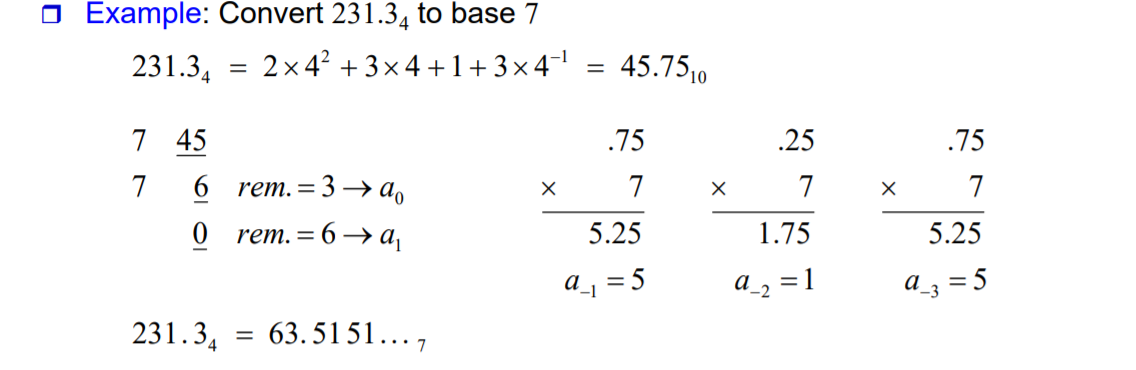
'전자기초 디지털논리설계' 카테고리의 다른 글
| Unit 3 - Boolean Algebra - 2 (0) | 2021.09.20 |
|---|---|
| Unit 2 - Boolean Algebra - 1 (0) | 2021.09.20 |
| Unit 1 - Binary Number(part 2) (0) | 2021.09.16 |



