Unit 1 - Binary Number(part 2)

디지털 시스템의 산술 연산은 일반적으로 이진법으로 수행됩니다. 이진 산술을 수행하는 논리 회로의 설계는 십진수보다 훨씬 쉽기 때문입니다.

덧셈과 곱셈 테이블이 훨씬 간단하다는 점을 제외하면 이진 산술은 십진법과 거의 같은 방식으로 수행됩니다.

Binary arithmetic in this unit: +, -, *, /

 

Binary Arithmetic

 

1. Addition

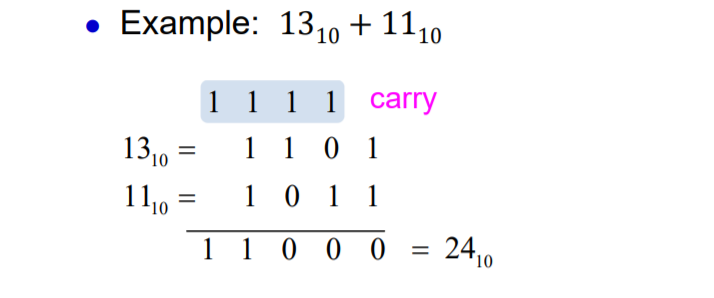
2. Substraction

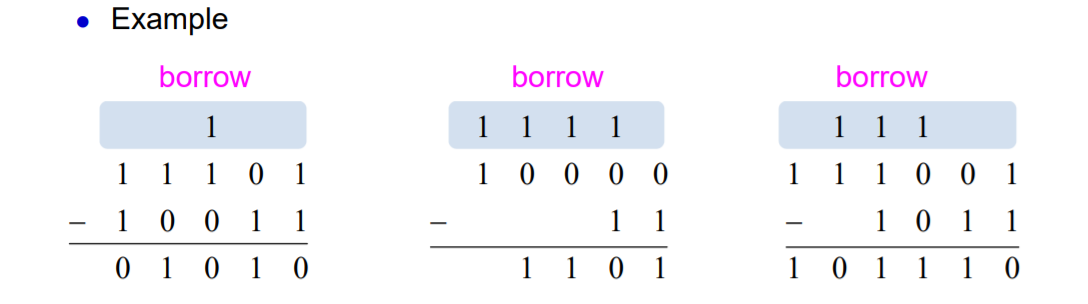
3. Multiplication(용어 기억)

4. Division(용어 기억)

우리는 음수값 없이는 뺄 수 없다는 것을 알았으므로 제수를 한 칸 오른쪽으로 이동하고 다시 시도합니다. 10010 에서 11011을 뺐을 때, 111의 값이 나왔습니다. 그래서 몫의 첫번째 부분에 10010의 위에 1을 적어줍니다. 그 후에 다음 0을 내려서 1110과 1011을 뺍니다. 1110과 1011을 뺐을 때, 11의 값이 나오니 2번째 몫은 1입니다. 다음에는 0을 하나 내렸을때 110이지만, 1011로 뺄수 없음으로 3번째 몫은 0이되고 1을 하나 더 내립니다. 1101과 1011의 결과는 10입니다. 따라서 몫에 1을 하나 추가하고 10은 나머지가 됩니다. 따라서 몫은 1101, 나머지는 10이 됩니다.

 

///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

 

Representation of Negative Numbers

 

지금까지는 양수로만 수를 다뤘습니다 이를 unsigned positive number 라고 합니다.

대부분의 컴퓨터에서는 양수와 음수가 모두 있습니다. 이를 signed number라고 합니다. 첫번째 수의 bit가 부호를 나타내는데 0 -> +(plus) , 1 -> -(minus)를 의미합니다.

 

Signed number를 표시하는 방법은 2가지입니다.

             n = 64일때, 즉 64bit일 때는 모든 수가 64bit로 표현된다.  

             컴퓨터에서는 연산을 할 때 모든 데이터의 크기는 같아야하기에 325 + 12가 아닌 325 + 012로 표현된다. 

             X + Y = Z 일 때 모든 데이터의 크기가 같아야한다.

 Unisgned number의 경우에는 전부 크기를 나타내는데 사용하는 반면, Signed number는 앞의 한자리는 부호를 나타내는 데 사용한다. 나머지는 Magnitude를 나타내는데 사용한다.

 

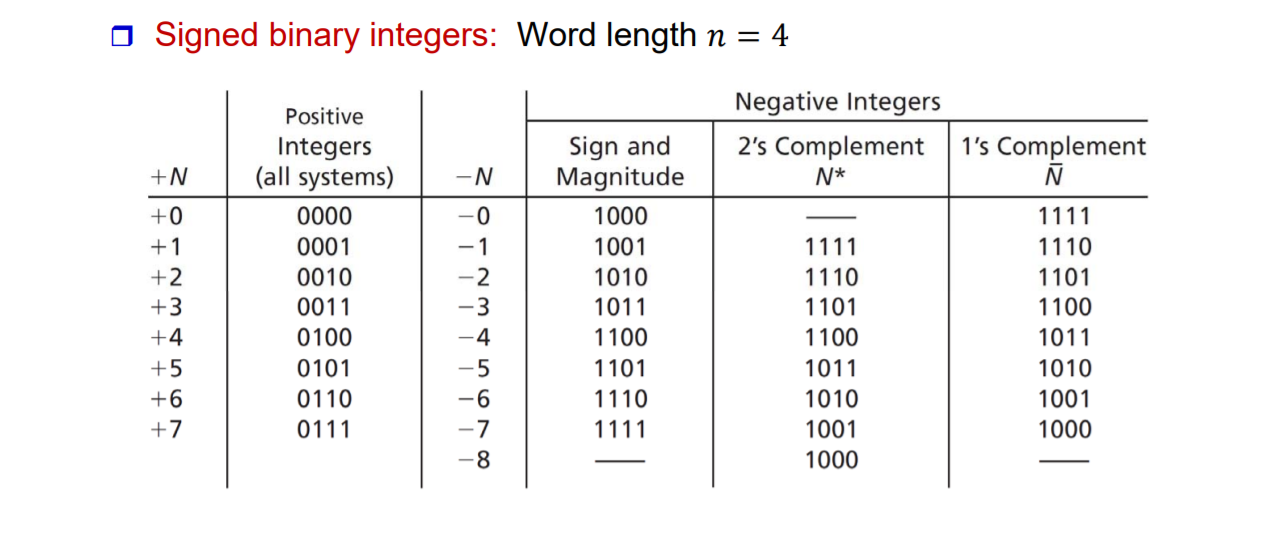
Negative Integers 에서 Sign and Magnitude는 Positive Integers과는 부호는 다르지만 3bit는 같은 것을 볼 수 있다.

하지만 2's, 1's complement는 다른 것을 볼 수 있다. 

 

1. Sign and Magnitude Number

1. N bit의 word는 positive integers는 (0 ~ 2^N-1), negative integers는 (-0 ~ -(2^N-1))까지 나타낼 수 있다.
2. 0과 -0의 표시가 있기에 조심해야한다. 따라서 정수 계산이 아닌 Real number 계산에 사용한다.

2. 2's complement Number

1. Positive number를 표시하는 것은 sign and magnitude 방법과 같다.
2. Negative number일 경우 N* = 2^N - N으로 mapping 된다.                                                                    예를 들어 n = 4일 경우 0 ~ 7은 그대로지만, -1 ~ -7은 16이 더해진 15 ~ 9까지 mapping이 된다. 이때 8은 -8을 사용해 8을 표시한다. 이는 sign and magnitude 방법과 비교해 -8을 하나더 사용할 수 있다. 

-0가 없다. 왜냐하면 16을 더했을때 4biit를 넘어가기 때문이다.

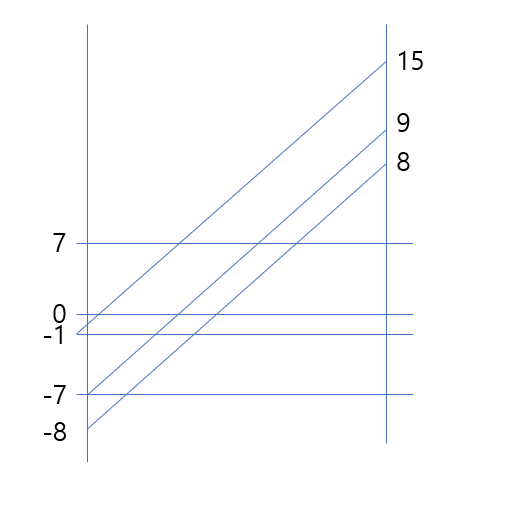
3. 1's complement Number

1. Positive number를 표시하는 것은 sign and magnitude 방법과 같다.
2. Negative number일 경우 N_ = (2^N - 1) - N으로 mapping 된다.                                                            예를 들어 n = 4일 경우 0 ~ 7은 그대로지만, -1 ~ -7은 15이 더해진 14 ~ 8까지 mapping이 된다. 이때 15은 0을 사용해 15을 표시한다. 이때 0이 1111, 0000인 2가지 표현이 생긴다.

0이 15가 더해져 15를 나타내는 모습이다.

 

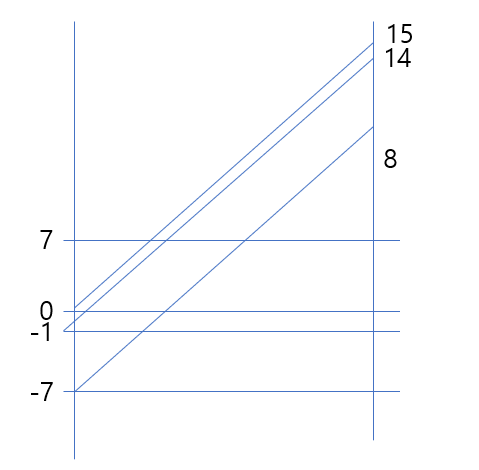
3가지 방법의 비교

3가지 방법의 비교

왼쪽에서 처음으로 1이 나왔을때를 찾은 뒤, 그 후부터 보수를 취해주면 쉽게 구할 수 있다. 1's comp 도 2's 와 같이 크기를 구할 수 있다. 

///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

 

1. 2's complements number 간의 addition

1. 위에서 강조했듯이 X + Y = Z일 때, X,Y,Z는 모두 같아야한다.(ex) 모두 8비트로 같아야한다.                          carry out이 발생했을 경우 -> 해당 위치가 무시된다.
2. 덧셈에서 overflow 없이 표현하려면 n+1 비트가 필요하다. n 비트끼리 더해서 표현할 수 있는 수를 넘었을 때 overflow가 발생한다.

negative + negative = positive 혹은 그 반대일 경우 overflow가 발생했음을 알 수 있다.

 

Case 4, 5에서 Carry out이 발생한 이유 

 -> -5는 -5 + 2^4 이다. -5 + 6 + 2^4이 되는데 이때 2^4을 빼줘야한다. -> carry out을 버린다.

 -> -3는 -3 + 2^4 이다. -4는 -4 + 2^4이다. 즉 -7 + 2^4*2가 되는데 이때 2^4를 빼준다 -> carry out을 버린다.

 

 

2. 1's complement number 간의 addition

1. 2's와 비슷하지만, carry out이 생길 경우 맨 오른쪽에 더해준다. -> end-around-carry라고 한다.

case 1,2는 2's와 같다.

 

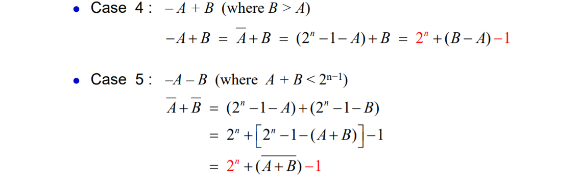
Case 4,5 에서 end-around-carry가 생긴 이유

 -> -5의 경우 -5 + 2^4 - 1이다. -5 + 6 + 2^4 - 1인데 2^4를 빼주면 -1이 남으니, 이때 1를 더해주는 것이다.

 -> -3의 경우 -3 + 2^4 - 1이다. -4의 경우 -4 + 2^4 - 1이다. 여기서 2^4를 빼주면서 1를 더해줘서 2^4 - 1만 남긴          것이다. (음수는 2^4 - 1을 가지고 있음으로)

 

overflow가 발생한 경우 + sign extension -> 더 많은 비트를 표현해야할 때, 가장 왼쪽의 값으로 늘린다.

///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////

 

Binary Codes

 

컴퓨터는 2진수에 대해서 연산을 하지만 우리는 10진수를 주로 쓴다. 따라서 컴퓨터 내에서는 10진수를 2진수로 변환하는 방법이 있어야한다. 이때 가장 많이 쓰는 것이 BCD(Binary Coded Decimal)이다.

4bit로 표현된 것을 볼 수 있다. 이때 10~15는 사용하지 않는다. (Not valid하다)

일반적으로 컴퓨터에서 가장 기본적인 데이터 단위는 byte이다. 1 byte = 8 bit이다. 이때 반으로 나누면 4 + 4 byte이다.

그렇다면 1 byte에는 2개의 BCD를 저장할 수 있다. 이것을 Packed BCD라고 한다.

왼쪽을 사용하지 않고 오른쪽 4bit만 사용하는 것이 Unpacked BCD하고 한다.

 

 

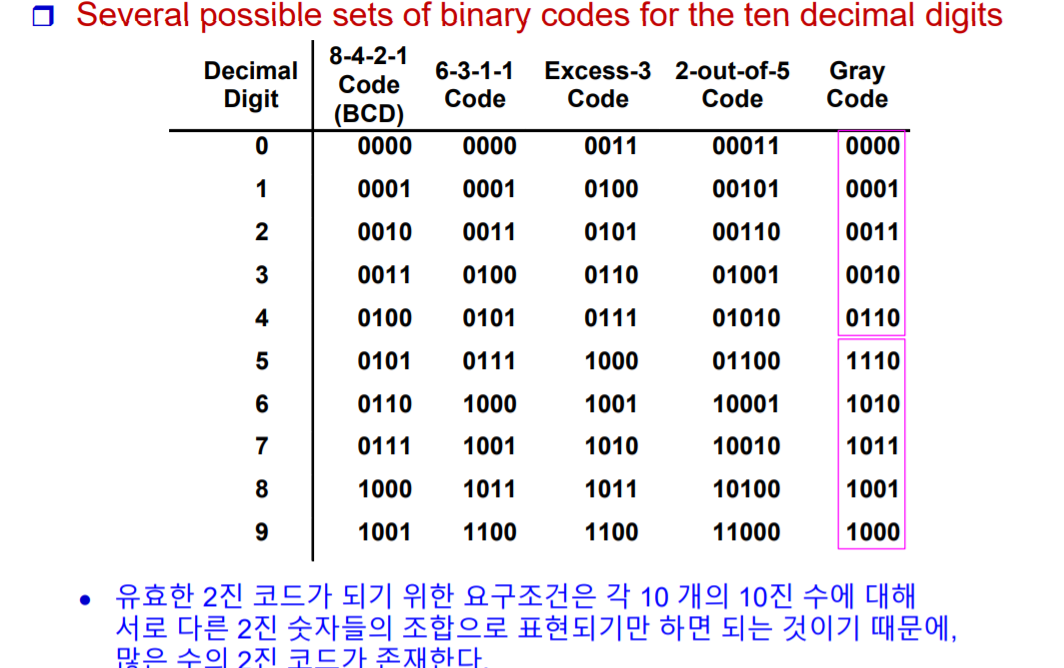
1. 8 - 4 - 2 - 1 Code(BCD)

1. 4bit로 표현되는데 가장 오른쪽부터 순서대로 Weight가 1, 2, 4, 8이기에 8-4-2-1로 쓰인다.

2. Excess - 3 Code

1. BCD에서 +3을 한 값이다. 따라서 0이 3, 1이 4로 표현된 것을 볼 수 있다.

3. 2 - out - of - 5 Code

1. 5bit중에서 1이 항상 2개이다. 2개의 1로 수를 표현하는 체계이다.
2. 오류가 발생하면 1의 갯수가 1 or 3개가 된다 -> 오류가 발생했다는 것을 쉽게 알 수 있다.

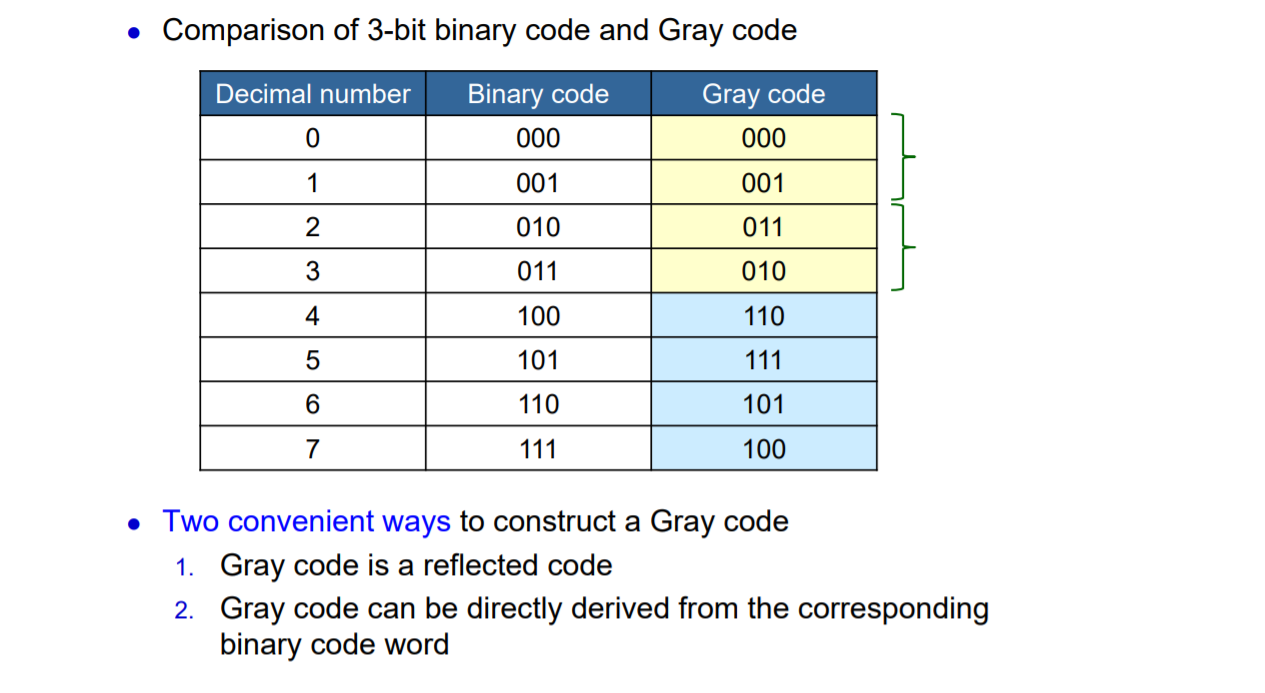
4. Gray Code

1. 인접된 bit가 1개만 다르다. 1과 0을 비교했을 때, 7과 8을 비교했을 때 모두 1개만 차이난다.
2. 회로 설계에서 많이 사용된다.
3. 반으로 나눴을 때(0~4, 5~9) 3bit 자리는 0과 1로 다르고, 나머지 3개의 bit는 mirror image임을 알수 있다.

참고해주세요

Gray Code : 

gray code 특징